Table of contents
In this article, we will cover the below-mentioned topics. If you want to learn Sorting in detail, do check out our Free Course on Sorting Algorithms in C for beginners. In this course, you will understand Sorting Algorithms and their Analysis. You will start by understanding Bubble Sort, how it works, modified Bubble sort, and its implementation. Then you will understand Selection Sort, its implementation, and analysis. Then we will understand Insertion Sort followed by Quick Sort. Then we will conclude our course with Merge Sort, its demonstration, implementation, and analysis along with time and space complexity.
- What is Merge sort
- Pseudocode for Merge sort
- Merge sort Algorithm
- Merge sort Algorithm Dry Run
- Time complexity of Merge sort
- Space complexity of Merge sort
- Merge sort program in C
- Merge sort in Java
- Merge sort in C++
- Merge sort in Python
- Merge sort example
- Difference between Quick sort and Merge sort
What is Merge sort
Merge sort is one of the most efficient sorting techniques and it’s based on the “divide and conquer” paradigm.
- In merge sort, the problem is divided into two subproblems in every iteration.
- Hence efficiency is increased drastically.
- It follows the divide and conquer approach
- Divide break the problem into 2 subproblem which continues until the problem set is left with one element only
- Conquer basically merges the 2 sorted arrays into the original array
Pseudocode for MergeSort
- Declare left and right var which will mark the extreme indices of the array
- Left will be assigned to 0 and right will be assigned to n-1
- Find mid = (left+right)/2
- Call mergeSort on (left,mid) and (mid+1,rear)
- Above will continue till left<right
- Then we will call merge on the 2 subproblems
Merge sort Algorithm
MergeSort(arr, left, right):
if left > right
return
mid = (left+right)/2
mergeSort(arr, left, mid)
mergeSort(arr, mid+1, right)
merge(arr, left, mid, right)
end
Merge sort Algorithm Dry Run
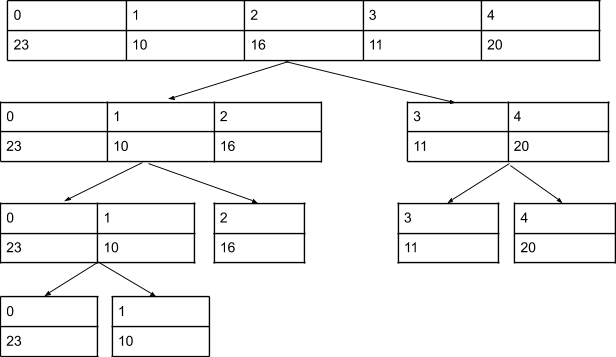
Time Complexity of Merge sort
- In the worst case, in every iteration, we are dividing the problem into further 2 subproblems. Hence this will perform log n operations and this has to be done for n iteration resulting in n log n operations total.
- In the best case that is sorted array, we can do some modification by using a flag to check whether the lament is already sorted or not
- Best Time Complexity: O(nlogn)
- Average Time Complexity: O(nlogn)
- Worst Time Complexity: O(nlogn)
Space Complexity of Merge sort
- n auxiliary space is required in Merge Sort implementation as all the elements are copied into an auxiliary array
- Hence space complexity is: O(n)
Merge sort program in C
#include <stdio.h>
void merge(int arr[], int start, int mid, int end) {
int len1 = mid - start + 1;
int len2 = end - mid;
int leftArr[len1], rightArr[len2];
for (int i = 0; i < len1; i++)
leftArr[i] = arr[start + i];
for (int j = 0; j < len2; j++)
rightArr[j] = arr[mid + 1 + j];
int i, j, k;
i = 0;
j = 0;
k = start;
while (i < len1 && j < len2) {
if (leftArr[i] <= rightArr[j]) {
arr[k] = leftArr[i];
i++;
} else {
arr[k] = rightArr[j];
j++;
}
k++;
}
while (i < len1) {
arr[k] = leftArr[i];
i++;
k++;
}
while (j < len2) {
arr[k] = rightArr[j];
j++;
k++;
}
}
void mergeSort(int arr[], int start, int end) {
if (start < end) {
int mid = start + (end - start) / 2;
mergeSort(arr, start, mid);
mergeSort(arr, mid + 1, end);
merge(arr, start, mid, end);
}
}
void display(int arr[], int size) {
for (int i = 0; i < size; i++)
printf("%d ", arr[i]);
printf("n");
}
int main() {
int arr[] = {6, 5, 12, 10, 9, 1};
int size = sizeof(arr) / sizeof(arr[0]);
printf("Original arrayn");
display(arr, size);
mergeSort(arr, 0, size - 1);
printf("Sorted arrayn");
display(arr, size);
}
Output of the program: Original array 6 5 12 10 9 1 Sorted array 1 5 6 9 10 12
Click here to know Quick Sort Algorithm using C , C++, Java, and Python
Merge sort in Java
class MergeSort {
void merge(int arr[], int left, int mid, int right) {
int len1 = mid - left + 1;
int len2 = right - mid;
int leftArr[] = new int[len1];
int rightArr[] = new int[len2];
for (int i = 0; i < len1; i++)
leftArr[i] = arr[left + i];
for (int j = 0; j < len2; j++)
rightArr[j] = arr[mid + 1 + j];
int i, j, k;
i = 0;
j = 0;
k = left;
while (i < len1 && j < len2) {
if (leftArr[i] <= rightArr[j]) {
arr[k] = leftArr[i];
i++;
} else {
arr[k] = rightArr[j];
j++;
}
k++;
}
while (i < len1) {
arr[k] = leftArr[i];
i++;
k++;
}
while (j < len2) {
arr[k] = rightArr[j];
j++;
k++;
}
}
void mergeSort(int arr[], int start, int right) {
if (start < right) {
int mid = (start + right) / 2;
mergeSort(arr, start, mid);
mergeSort(arr, mid + 1, right);
merge(arr, start, mid, right);
}
}
static void display(int arr[]) {
int n = arr.length;
for (int i = 0; i < n; ++i)
System.out.print(arr[i] + " ");
System.out.println();
}
public static void main(String args[]) {
int arr[] = { 6, 5, 12, 10, 9, 1 };
MergeSort ob = new MergeSort();
System.out.println("Original array");
display(arr);
ob.mergeSort(arr, 0, arr.length - 1);
System.out.println("Sorted array");
display(arr);
}
}
Output of the program: Original array 6 5 12 10 9 1 Sorted array 1 5 6 9 10 12
Merge sort in C++
#include <iostream>
using namespace std;
void merge(int arr[], int start, int mid, int end) {
int len1 = mid - start + 1;
int len2 = end - mid;
int leftArr[len1], rightArr[len2];
for (int i = 0; i < len1; i++)
leftArr[i] = arr[start + i];
for (int j = 0; j < len2; j++)
rightArr[j] = arr[mid + 1 + j];
int i, j, k;
i = 0;
j = 0;
k = start;
while (i < len1 && j < len2) {
if (leftArr[i] <= rightArr[j]) {
arr[k] = leftArr[i];
i++;
} else {
arr[k] = rightArr[j];
j++;
}
k++;
}
while (i < len1) {
arr[k] = leftArr[i];
i++;
k++;
}
while (j < len2) {
arr[k] = rightArr[j];
j++;
k++;
}
}
void mergeSort(int arr[], int start, int end) {
if (start < end) {
int mid = start + (end - start) / 2;
mergeSort(arr, start, mid);
mergeSort(arr, mid + 1, end);
merge(arr, start, mid, end);
}
}
void display(int arr[], int size) {
for (int i = 0; i < size; i++)
cout << arr[i] << " ";
cout << endl;
}
int main() {
int arr[] = {6, 5, 12, 10, 9, 1};
int size = sizeof(arr) / sizeof(arr[0]);
cout << "Original array n";
display(arr, size);
mergeSort(arr, 0, size - 1);
cout << "Sorted array n";
display(arr, size);
return 0;
}
Output of the program: Original array 6 5 12 10 9 1 Sorted array 1 5 6 9 10 12
Merge sort in Python
def mergeSort(arr):
if len(arr) > 1:
r = len(arr)//2
leftArr = arr[:r]
rightArr = arr[r:]
mergeSort(leftArr)
mergeSort(rightArr)
i = j = k = 0
while i < len(leftArr) and j < len(rightArr):
if leftArr[i] < rightArr[j]:
arr[k] = leftArr[i]
i += 1
else:
arr[k] = rightArr[j]
j += 1
k += 1
while i < len(leftArr):
arr[k] = leftArr[i]
i += 1
k += 1
while j < len(rightArr):
arr[k] = rightArr[j]
j += 1
k += 1
def display(arr):
for i in range(len(arr)):
print(arr[i], end=" ")
print()
if __name__ == '__main__':
arr = [6, 5, 12, 10, 9, 1]
print("Original array")
display(arr)
mergeSort(arr)
print("Sorted array")
display(arr)
Output of the program: Original array 6 5 12 10 9 1 Sorted array 1 5 6 9 10 12
Click here to know Quick Sort Algorithm using C , C++, Java, and Python
Merge Sort Example
Merge 2 sorted array
Input:
1 5 8 10 20
4 6 9 15 40 55 92Output:
1 4 5 6 8 9 10 15 20 40 55 92
JAVA Code
import java.io.*;
class Merge {
static int[] merge(int[] arr1, int[] arr2, int n, int m){
int ans[]=new int[n+m];
int i=0,j=0,k=0;
while(i<n && j<m){
if(arr1[i]<arr2[j])
ans[k++]=arr1[i++];
else
ans[k++]=arr2[j++];
}
while(i<n)
ans[k++]=arr1[i++];
while(j<m)
ans[k++]=arr2[j++];
return ans;
}
static void display(int[] arr){
for(int i=0;i<arr.length;i++)
System.out.print(arr[i]+" ");
}
public static void main (String[] args) {
int[] arr1={1,5,8,10,20};
int[] arr2={4,6,9,15,40,55,92};
int[] ans = merge(arr1,arr2,arr1.length,arr2.length);
display(ans);
}
}
C++ Code
#include <iostream>
using namespace std;
void merge(int arr1[], int arr2[], int n, int m){
int ans[n+m];
int i=0,j=0,k=0;
while(i<n && j<m){
if(arr1[i]<arr2[j])
ans[k++]=arr1[i++];
else
ans[k++]=arr2[j++];
}
while(i<n)
ans[k++]=arr1[i++];
while(j<m)
ans[k++]=arr2[j++];
for(int i=0;i<n+m;i++)
cout<<ans[i]<<" ";
}
int main () {
int arr1[]={1,5,8,10,20};
int arr2[]={4,6,9,15,40,55,92};
merge(arr1,arr2,sizeof(arr1)/sizeof(arr1[0]),sizeof(arr2)/sizeof(arr2[0]));
return 0;
}
C Code
#include <stdio.h>
void merge(int arr1[], int arr2[], int n, int m){
int ans[n+m];
int i=0,j=0,k=0;
while(i<n && j<m){
if(arr1[i]<arr2[j])
ans[k++]=arr1[i++];
else
ans[k++]=arr2[j++];
}
while(i<n)
ans[k++]=arr1[i++];
while(j<m)
ans[k++]=arr2[j++];
for(int i=0;i<n+m;i++)
printf("%d ",ans[i]);
}
int main () {
int arr1[]={1,5,8,10,20};
int arr2[]={4,6,9,15,40,55,92};
merge(arr1,arr2,sizeof(arr1)/sizeof(arr1[0]),sizeof(arr2)/sizeof(arr2[0]));
return 0;
}
Difference between QuickSort and MergeSort
- In terms of algorithm and complexity
- In Quicksort, the partition of the array in the next iteration completely depends on the choice of the pivot element. We will have 2 arrays after placing the pivot to its correct position. So if we have a sorted array, the pivot will remain at the same position, leading to n^2 complexity, as no real partition will take place.
- In Mergesort, we take the mid index which is (beg index + end index)/2. Our array will always break into two subsequent arrays with approximately equal length. This keeps the complexity to n log n and is much time-efficient
- In terms of space complexity
- If we are implementing our sort algorithm using recursion, then obviously our recursion stack will take n space.
- But in merge sort in every iteration, we create two new temporary arrays. In one we copy all the left subarray and in other, we copy all the right subarray. Since all the elements are copied, it takes another n space.
- In quicksort no such temporary array creation and copying takes place. Therefore no extra n space is needed
- In terms of speed
- Quicksort is faster than the merge sort because of previous explanation.
- No temporary array, copying, etc happens in quicksort, making it much faster in execution
- In terms of in-place
- In-place states that the algorithm is in-place if it does not need extra memory barring some variable creation which counts to constant space.
- Quicksort is in place but merge sort is not as it needs extra n space for creating temporary arrays whose sixes adds up to n
- In terms of stability
- Stability states that the algorithm is stable if the relative ordering of the same elements in the input and output array remains the same.
- In quicksort, a lot of swapping takes place leading it to lose its stability whereas the merge sort maintains the relative ordering, and hence it is stable.
| QUICK SORT | MERGE SORT |
| Splitting of the array depends on the value of pivot and other array elements | Splitting of array generally done on half |
| Worst-case time complexity is O(n2) | Worst-case time complexity is O(n log n) |
| It takes less n space than merge sort | It takes more n space than quicksort |
| It works faster than other sorting algorithms for small data set like Selection sort etc | It has a consistent speed on any size of data |
| It is in-place | It is out-place |
| Not stable | Stable |
This brings us to the end of this article where we learned about merge sort and its implementation in various languages.
A certificate will improve your chances of getting recognized in the industry. Check out Great Learning’s PG program in Data Science and Business Analytics to upskill in the domain. This course will help you learn from a top-ranking global school to build job-ready Data Science skills. This 6-month program offers a hands-on learning experience with top faculty and mentors. On completion, you will receive a Certificate from The University of Texas at Austin.
