- Fibonacci Series in Java without using recursion
- Fibonacci Series using recursion in Java
- Display Fibonacci Series Using For Loop
- Display Fibonacci series using While Loop
- Display the Fibonacci series up to a given number
- Conclusion
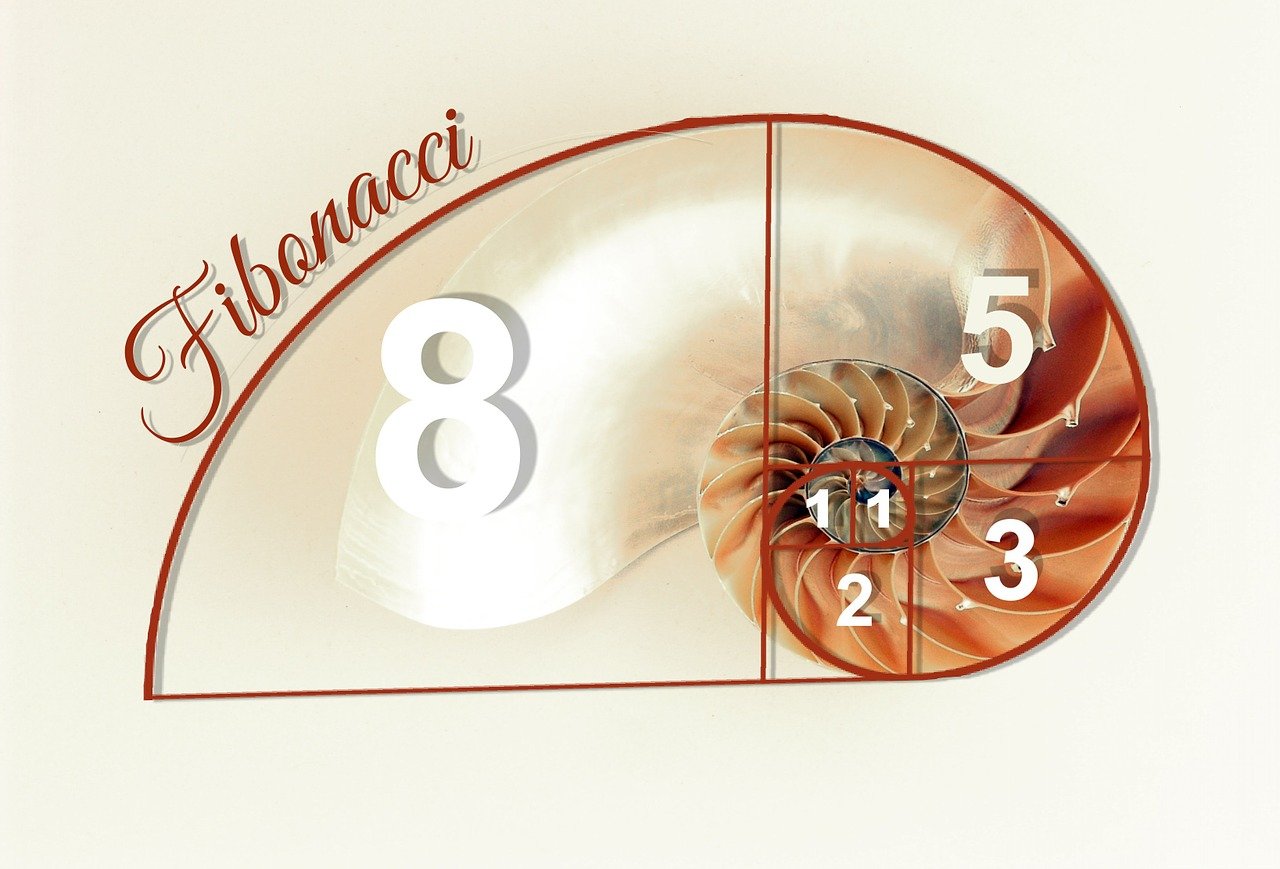
Fibonacci series refers to the series where the following number is the addition of the previous two numbers. The first two numbers of the series are usually 0 and 1.
Example
input= 9
output= 0,1,1,2,3,5,8,13,21
Here, the first number is 0 while the second is 1; hence, the next number would be the sum of these two numbers that is 0+1=1. Similarly 1+1=2; 1+2=3, 2+3=5; 3+5=8; 5+8=13; 8+13=21
There are different ways or methods to display the Fibonacci series.
Fibonacci Series in Java without using recursion
We can avoid the repeated work we performed in recursion by the dynamic programming method.
To perform this, we need first to create an array arr[] of size N. Then, we need to initialize the array as arr[0]=0; arr[1]=1. After this we iterate the value of i from 2 to N, and update the array arr[] as
arr[i]= arr[i-2] + arr[i-1].
Finally, we print the value N.
This syntax is the same as the original syntax of the Fibonacci series the only difference is that we have used an array.
The implementation is illustrated below:
class Fibonaccigreatlearning{
public static void main(String args[])
{
int n1=0,n2=1,n3,i,count=15;
System.out.print(n1+" "+n2);//printing 0 and 1
for(i=2;i<count;++i)//loop starts from 2 because 0 and 1 are already printed
{
n3=n1+n2;
System.out.print(" "+n3);
n1=n2;
n2=n3;
}
}}Output
0 1 1 2 3 5 8 13 21 34 55 89 144 233 377
In this case, the time complexity and Auxiliary space are the same: O (N).
Fibonacci Series using recursion in Java
There are some conditions satisfying which we can use recursion in Java.
Firstly we would need the number whose Fibonacci series needs to be calculated
Now recursively iterate the value from N to 1.
There are the following two cases in it:
Base case- here, if the value that is called is less than 1, then the function returns 1
Recursive call- the previous two values are called in case the base case is not met.
The syntax for which is as follows
recursive_function (N-1) + recursive_function (N-2);
There is also a term referred to as recursive function; it is called at each recursive call to return the previous two values for the recursive function.
Implementation:
class Fibonaccigreatlearning{
static int n1=0,n2=1,n3=0;
static void printFibonacci(int count){
if(count>0){
n3 = n1 + n2;
n1 = n2;
n2 = n3;
System.out.print(" "+n3);
printFibonacci(count-1);
}
}
public static void main(String args[]){
int count=20;
System.out.print(n1+" "+n2);//printing 0 and 1
printFibonacci(count-2);//n-2 because 2 numbers are already printed
}
}Output–
0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181
Here the time complexity and Auxiliary space are O(2^N) and O(1), respectively.
Display Fibonacci Series Using For Loop
This loop is the same as that of the while loop. Firstly, we initialize numbers for the first two digits, after which we print the series’s first term, hence computing the next term by the formula of Fibonacci. Finally, carry out further by assigning the value of the second term to the first term and the next term to the second term.
Implementation:
class greatlearning{
public static void main(String[] args) {
int n =17 ,firstTerm = 0, secondTerm = 1;
System.out.println("Fibonacci Series till " + n + " terms:");
for (int i = 1; i <= n; ++i) {
System.out.print(firstTerm + ", ");
// compute the next term
int nextTerm = firstTerm + secondTerm;
firstTerm = secondTerm;
secondTerm = nextTerm;
}
}
}Output
Fibanacci Series till 17 terms: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987
Display Fibonacci series using While loop
The while loop is the iterative function where the first and second numbers are 0 and 1, respectively. We print these numbers and then send them to the iterative while loop, where the next number is obtained by adding the previous two numbers. Then simultaneously, we swap the numbers where the first number is the second number and the second number becomes the third.
We can implement the while loop as below
// Java program for the above approach
class Greatlearning {
// Function to print N Fibonacci Number
static void Fibonacci(int N)
{
int num1 = 0, num2 = 1;
int counter = 0;
// Iterate till counter is N
while (counter < N) {
// Print the number
System.out.print(num1 + " ");
// Swap
int num3 = num2 + num1;
num1 = num2;
num2 = num3;
counter = counter + 1;
}
}
// Driver Code
public static void main(String args[])
{
// Given Number N
int N = 18;
// Function Call
Fibonacci(N);
}
}Output
0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1567
Here the time complexity and auxiliary spaces are O(N) and O(1), respectively.
Display the Fibonacci series up to a given number
In the previous cases, we defined the number of which we printed the Fibonacci series, but in this case, we print the series up to a number.
We do so by comparing the first number or term with n, and if the first number is proved to be less than n, then the number is printed in the series. If not so, then the series is assumed to be completed.
We can illustrate it as below
class greatlearning {
public static void main(String[] args) {
int n = 88, firstTerm = 0, secondTerm = 1;
System.out.println("Fibonacci Series Upto " + n + ": ");
while (firstTerm <= n) {
System.out.print(firstTerm + ", ");
int nextTerm = firstTerm + secondTerm;
firstTerm = secondTerm;
secondTerm = nextTerm;
}
}
}Output
Fibonacci series upto 88: 0, 1,1,2,3,5,8,13,21,34,55,
Conclusion
With this, we come to the end of this blog. Embark on a learning adventure like no other with our extensive collection of free online courses. Whether you’re interested in diving into the world of Cybersecurity, mastering the art of Management, exploring the wonders of Cloud Computing, or delving into the intricate realm of IT and Software, we have courses that cater to your interests and goals.
Engaging in the study of Java programming suggests a keen interest in the realm of software development. For those embarking upon this journey with aspirations towards a career in this field, it is recommended to explore the following pages in order to acquire a comprehensive understanding of the development career path:
